Особливості побудови логіки машини, що оминає перешкоди
Є два завдання, які треба вирішити: знайти вихід і оптимізувати зворотний шлях.
Для виявлення виходу можна керуватись методом лівої руки. Уявіть, що ви знаходитесь у лабіринті і постійно тримаєте ліву руку на стіні. Зрештую, це дозволить вам вийти із незамкнутого лабіринту. Робот працює тільки із незамкненими лабіринтами.
Спосіб лівої руки описується простими умовами:
- Якщо ви можете повернути ліворуч, поверніть ліворуч.
- Якщо ви можете рухатися прямо, рухайтеся прямо.
- Якщо ви можете повернути праворуч, поверніть праворуч.
- Якщо ви в глухому куті, розгорніться.
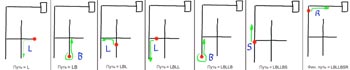
Робот повинен приймати рішення на перехресті. Якщо робот на повороті не повертає, він рухається прямо. Кожне рішення прийняте роботом записується в пам'яті для побудови оптимального зворотного маршруту
L = Лівий поворот
R = Правий поворот
S = Пропуск повороту
B = Розворот.
На зображенні вище показаний цей метод у дії. Шлях до виходу – це LBLLBSR.
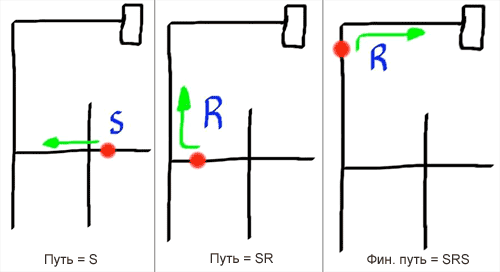
Ми повинні перетворити шлях LBLLBSR на оптимальний шлях SRR. Для цього необхідно знайти місце, де робот повернув не туди. "B" це розворот, який може статися в безвиході, тобто. на неправильному шляху. Щоб
оптимізувати шлях ми повинні замінити "B" на щось інше.
Давайте розглянемо перші 3 дії LBLLBSR – LBL. Замість того, щоб повернути ліворуч, розвернутися і знову повернути ліворуч, робот мав піти прямо. Отже, ми можемо сказати, що LBL = S.
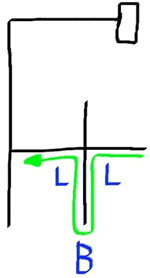
Ось повний список подібних замін:
LBR = B
LBS = R
RBL = B
SBL = R
SBS = B
LBL = S
У лабіринті можуть бути не всі ці повороти, але вони потрібні. Деякі навіть повертають B назад. Це потрібно для подальшої правильної оптимізації шляху.
LBL = S, новий шлях SLBSR. LBS = R, новий шлях SRR. Як ви бачите, ми отримали оптимальний шлях. Мій робот оптимізує шлях під час руху. Шлях зберігається в масиві, і щоразу перед збереженням ходу він перевіряє, що попередній хід не B, якщо В, то оптимізує шлях. Роботу необхідно знати принаймні 3 останніх ходи для оптимізації алгоритму проходження шляху.
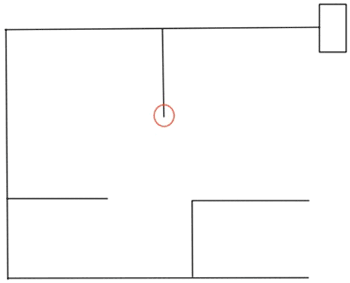
Розглянемо інший приклад.
Якщо використовувати правило лівої руки для наведеного вище лабіринту, то отримаємо наступний алгоритм: LLLBLLLRBLLBSRSRS
Починаємо скорочувати:
LL (LBL = S) LL (RBL = B) (LBS = R) RSRS = LLSLLBRRSRS
Продовжуємо:
LLSL (LBR = B) RSRS = LLSLBRSRS
Продовжуємо:
LLSBSRS
Продовжуємо:
LL (SBS = B) RS = LLBRS
Продовжуємо:
L (LBR = B)S = LBS
Разом:
LBS = R







Комментариев нет:
Отправить комментарий